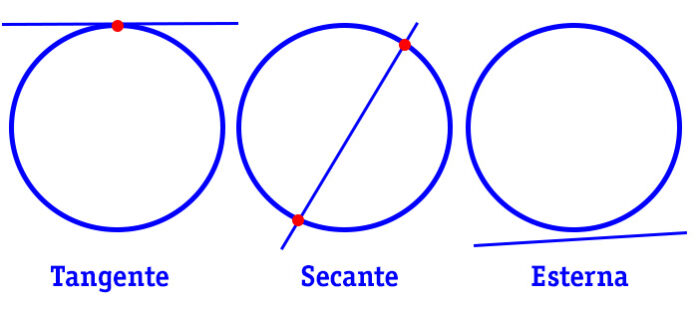
Disegniamo un cerchio. Ora tracciamo una linea retta. Può succedere che questa linea intersechi il cerchio disegnato prima, oppure no.
Cioè, a seconda di come abbiamo tracciato la linea, ci potrebbero essere due intersezioni sulla circonferenza, oppure una oppure nessuna intersezione. Le tre situazioni indicano in pratica che la retta sia secante, tangente o esterna alla circonferenza. In un problema di matematica scolastica, una volta date l’equazione della circonferenza e della linea, si possono trovare le coordinate delle intersezioni, o dell’unica intersezione, oppure si può dire che non ci sono intersezioni.
Fin qui, penso di non aver detto nulla di nuovo, però… c’è qualcosa da aggiungere. Se la nostra retta taglia la circonferenza in due punti, e noi la spostiamo piano piano da una parte, allora ci saranno ancora due punti di intersezione, fino a che si avvicinano e diventano un punto solo (il caso citato nel quale la retta è tangente al cerchio). Ma proviamo ad immaginare che i punti siano ancora due, solo che… coincidono. Allora possiamo rettificare la nostra frase di prima, dicendo che una retta interseca la circonferenza in due punti, che potrebbero anche coincidere, oppure non la interseca per niente. Ma, sognando un po’, proviamo a dire che se la retta non interseca la circonferenza, allora i due punti di intersezione “sono immaginari”. Cosa vi pare dell’idea? Adesso, con questo nostro sogno, possiamo dire che comunque tracciamo una circonferenza ed una retta, le intersezioni saranno sempre due, casomai immaginarie.
Certo, abbiamo lavorato di fantasia, ma (non restateci male), i matematici lavorano proprio così, infatti secondo la matematica, due rette si intersecano sempre, e se dovessero essere parallele, si intersecheranno in un punto immaginario; una retta e una circonferenza si intersecano sempre in due punti, casomai immaginari; anche due circonferenze si incontrano sempre in due punti, casomai immaginari, e così via.
Ma il bello è che, per ogni singolo problema, anche i punti immaginari hanno delle coordinate ben precise, e si possono calcolare con sistemi simili a quelli usati per i punti veri, reali. Quindi… esistono anche i punti immaginari? Certo, e siccome hanno delle coordinate ben precise, le equazioni che li coinvolgono vengono usati per risolvere problemi di matematica, della fisica, di elettronica e in tanti altri campi, e questi sono problemi reali. Quindi ecco che per fortuna esistono numeri immaginari, altrimenti non potremo risolvere problemi reali!
Giorgio Dendi